 Vinz_o.wav (214k) Originaldatei
Vinz_o.wav (214k) Originaldatei Vinz_s.wav (214k) Synthetika
Vinz_s.wav (214k) Synthetika Vinz_sn.wav (214k) Synthetika mit Rauschen
Vinz_sn.wav (214k) Synthetika mit RauschenNachfolgend soll an einem Beispiel gezeigt werden, dass der Klang einer Glocke in sehr guter Qualität synthetisch erzeugt werden kann. Als Quelle diente die Aufzeichnung des Klangs der Glocke "La Vinzelle" von 1870. Näheres siehe bei Bill Hibbert, wo sich die Datei vinz.mp3 (48k) befindet, die nach .wav konvertiert und auf rund 4 Sekunden zugeschnitten wurde. Diese Datei Vinz_o.wav diente als Ausgangsmaterial für die Analyse. Die vollständig synthetisch erzeugte Datei Vinz_s.wav sollte ihr möglichst nahe kommen. Abschließend wurde dieser noch als Vinz_sn.wav ein synthetisches Rauschen hinzugemischt. Um Missverständnissen vorzubeugen: Die Datei Vinz_s.wav wurde vom ersten bis zum letzten Bit ohne jeden Zugriff auf die Originaldatei auf rein rechnerischem Wege durch ein C-Programm erzeugt.
 Vinz_o.wav (214k) Originaldatei
Vinz_o.wav (214k) Originaldatei
 Vinz_s.wav (214k) Synthetika
Vinz_s.wav (214k) Synthetika
 Vinz_sn.wav (214k) Synthetika mit Rauschen
Vinz_sn.wav (214k) Synthetika mit Rauschen
Eine detaillierte Analyse der Originaldatei zeigt rund 20 Teiltöne, von denen 16 für die Synthese benutzt wurden:
| 114.10 Hz | B -17ct | Resonanzton 1) |
| 155.12 Hz | es0 +15ct | Unterton |
| 309.97 Hz | es1 +13ct | Prim |
| 364.09 Hz | ges1 -8ct | Terz |
| 469.74 Hz | b1 +33ct | Quint |
| 605.65 Hz | es2 -27ct | Oktav 4' |
| 798.67 Hz | as2 -48ct | Quart 4' |
| 819.82 Hz | as2 -3ct | Quart 4' |
| 906.43 Hz | b2 -29ct | Quint 4' |
| 1012.18 Hz | c3 -38ct | Sext 4' |
| 1248.52 Hz | es3 +25ct | Oktav 2' |
| 1622.52 Hz | as3 -21ct | Quart 2' |
| 2518.35 Hz | es4 +40ct | Oktav 1' |
| 2598.95 Hz | e4 -5ct | Non 1' 2) |
| 2798.86 Hz | f4 +23ct | Non 1' 2) |
| 2998.79 Hz | ges4 +42ct | Dezim 1' 2) |
Dass sich der Gesamtklang aus der additiven Überlagerung der Teiltöne ergibt, versteht sich von selbst. Die Kunst der Synthese besteht nun darin, den zeitlichen Amplitudenverlauf für jeden einzelnen Teilton möglichst gut nachzubilden. Es hat sich gezeigt, dass dieser Amplitudenverlauf - auch 'Einhüllende' (engl. 'envelope') genannt - gut approximiert werden kann, indem man diese Funktion durch eine additive Überlagerung einer e-Funktion mit mehreren (3 bis 7, je nach mehr oder weniger filigranem Amplitudenverlauf) gedämpften Sinusschwingungen darstellt, wobei die Bestimmung der Koeffizienten dieser Sinusfunktionen eine recht mühsame Angelegenheit ist. Im vorliegenden Fall wurden die Koeffizienten mit Hilfe einer Tabellenkalkulation in aufwändiger Kleinarbeit durch schrittweise Annäherung bestimmt. Eine algorithmische Bestimmung der 10 bis 18 Koeffizienten eines Teiltonamplitudenverlaufs über die Minimierung der Quadratsumme im Gaußschen Sinne scheitert bisher an massiven Konvergenzproblemen, d. h. es gibt eine Unzahl lokal eng begrenzter Minima. Sind die Koeffizienten zur Beschreibung der Amplitudenverläufe der Teiltöne gefunden, so ist der Rest eine triviale Programmierübung. Es wurden folgende Gleichungen verwendet:
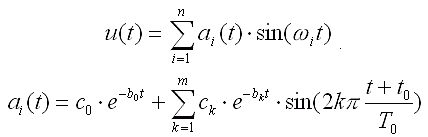
Abschließend sei noch darauf hingewiesen, dass synthetisierte Glockenklänge häufig am Anfang ein Ploppen aufweisen, obwohl der Signalverlauf sauber erscheint. Dagegen kann man einen kleinen Trick verwenden: Nach erfolgter Berechnung des Gesamtsignals dämpft man dieses am Anfang, indem man vom Beginn bis zu 2...5 Millisekunden (ausprobieren) mit einem von 0 bis 1 stetig ansteigenden Faktor multipliziert.
 (52k)
(52k)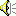 (52k)
(52k)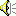 (52k)
(52k)© J. Grabinski 2006